Current activities
The ODEN group for Applied Mathematics (AMG) is an interdisciplinary research effort from departments including Mathematics, Statistics, Physics and Computer Science. We focus our research on the modeling, classical and statistical analysis and numerical simulations of non-linear phenomena. Some of the current research projects include a wide range of theoretical and computational aspects of mathematical models from non-linear dynamics for classical and semi classical fluid systems as well as quantum and statistical transport dynamics in biological systems.
More specifically, projects focus on different aspects related to:
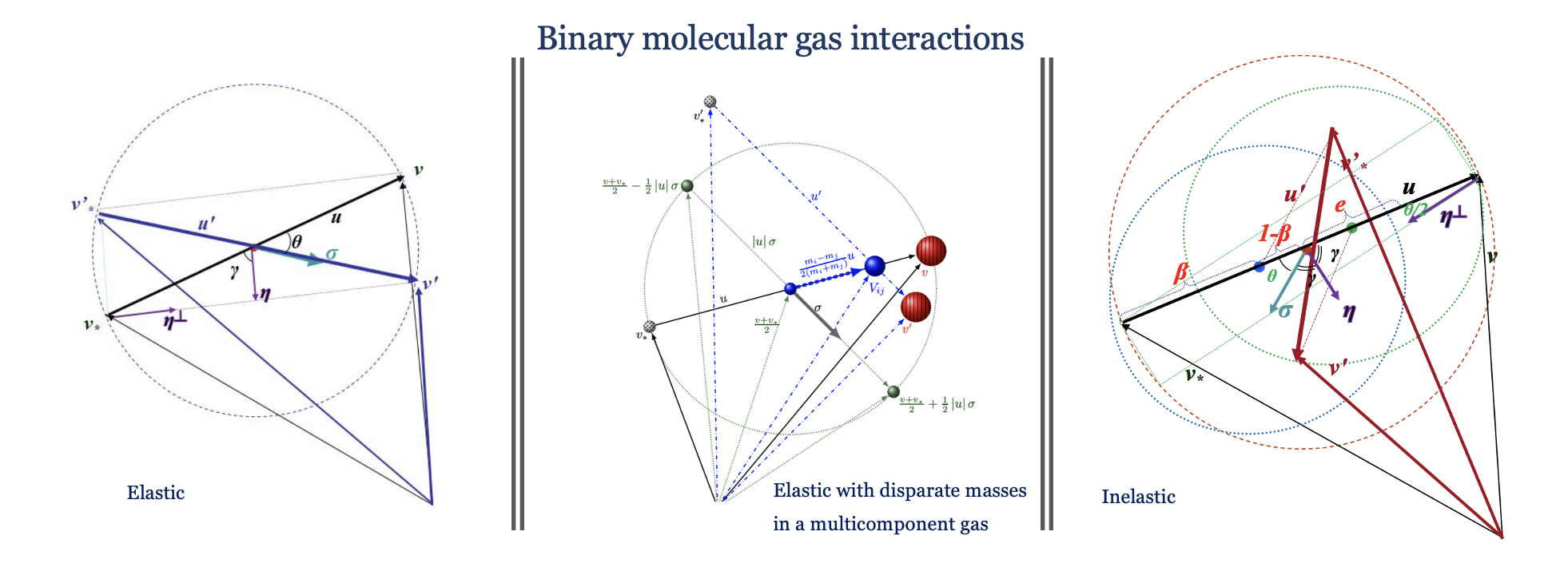
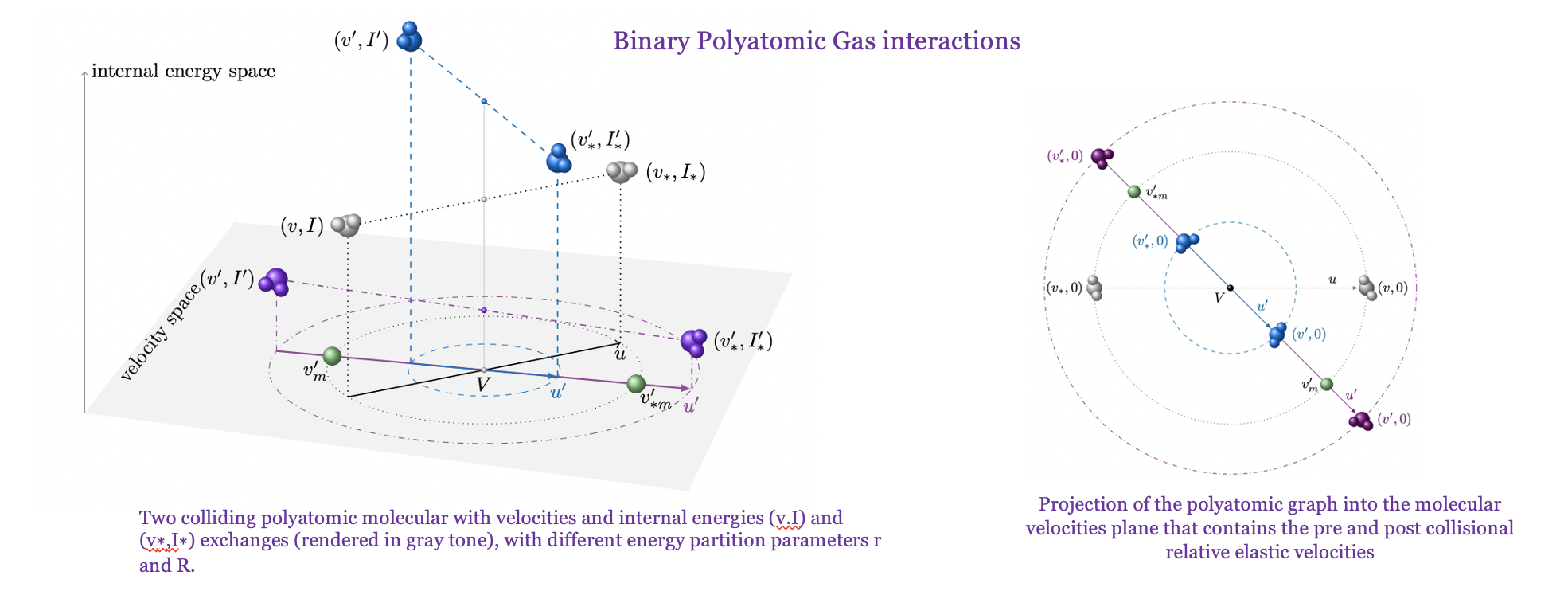
- Kinetic collisional theory for rarefied gas regimes in multicomponent mixtures and polyatomic gases, plasma dynamics in collisionless and collisional regimes under strong electric or magnetization effects.Cha rged particle transport emphasizing the linking of quantum, statistical and fluid mechanical states.
- Conservative numerical algorithms for Boltzmann and Landau flows in particle physics, multicomponent gas systems, turbulence gas flow simulations induced by wall thermalization; simulation of swarm and flocking dynamics with random dissipation to equilibrium states.
- Numerical algorithms and analysis of advection-diffusion equations, for modeling systems that are advection dominated and contain degenerate diffusion. General finite element development and analysis, especially finite elements defined over quadrilaterals and hexahedra. Applications to Modeling of the Earth’s mantle, in the presence of partial melting.
- Premixed and non-premixed turbulent combustion models in spatial-temporal periodic and randomly heterogeneous media.
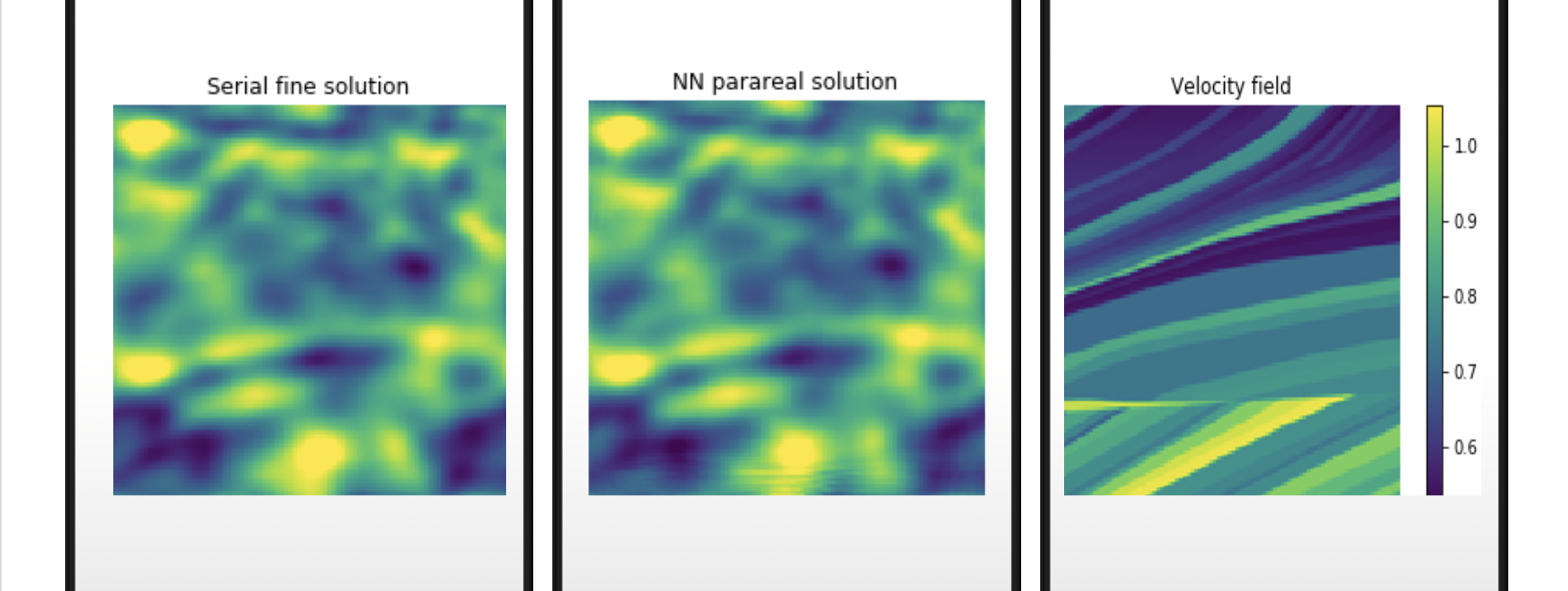
- Multiscale modeling in high frequency wave propagation. Deep learning theory and algorithms for differential games and other scientific computing problems and Integral geometry and application to data sampling
- Characterization of geometric manifold structures and model dynamical processes using the interplay of embedded symmetry, smoothness, encoded information, and uncertainty.
- Signal processing applied harmonic analysis, compressed sensing, theoretical computer science, and machine learning.
- Analysis of randomized embeddings used to overcome the computational challenges associated with problems set in high dimensional spaces. Applications to data analysis, computational statistics, geometry of data-sets in high dimensional spaces, etc. Modeling of acoustic and electromagnetic scattering using tools from computational harmonic analysis.
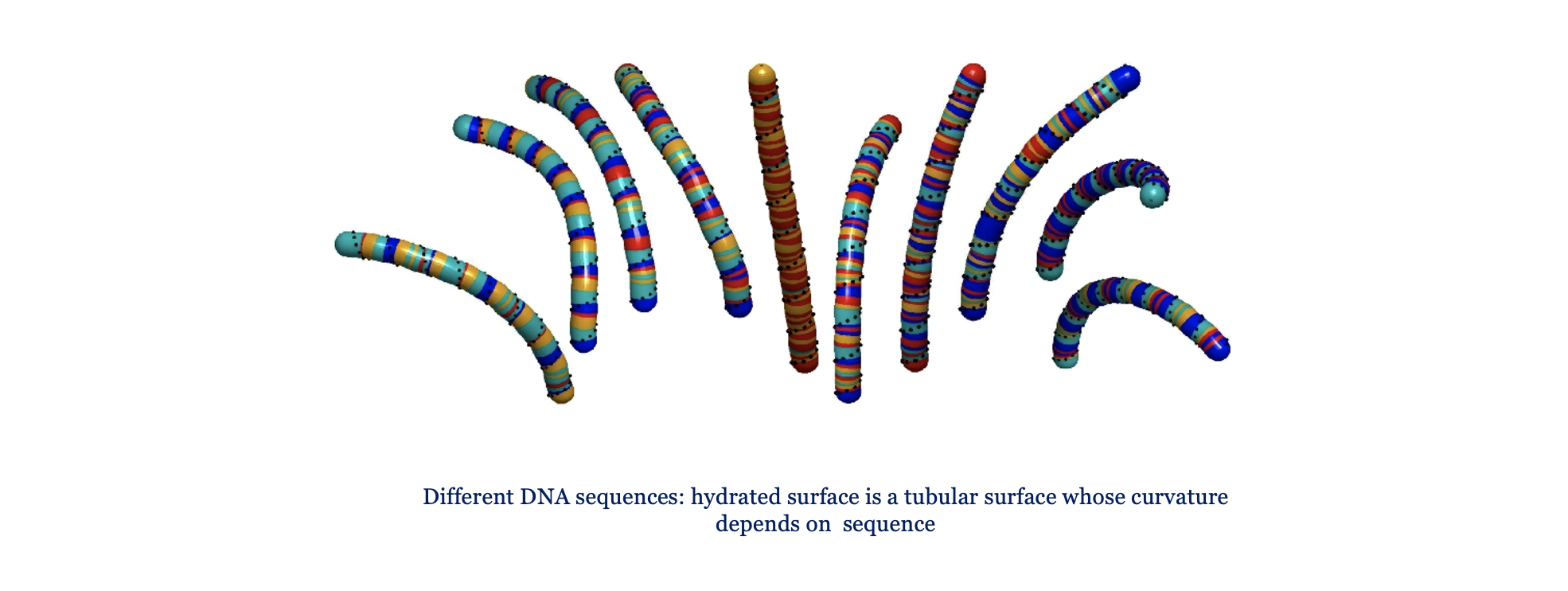
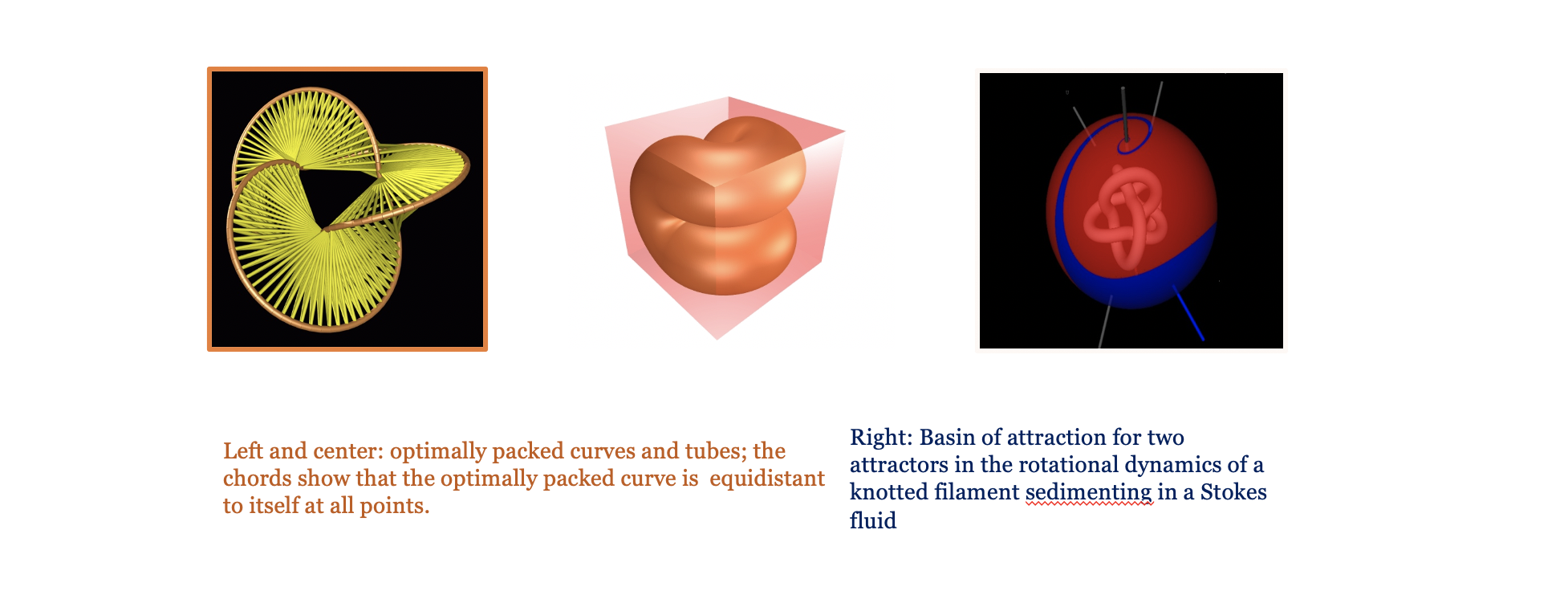
- Geomechanics, aerodynamics, biological and molecular dynamics. Models for DNA structure prediction, fluid-structure interaction, hydrodynamic transport and diffusion, boundary integral equations, optimal packing of curves with finite thickness, applied analysis in continuum mechanics.
- Mathematical epidemiology by network-based for spread prediction of infectious diseases and theoretical evolutionary dynamics in biology.
- Statistical methods on the development and analysis of simulation-based methods for Bayesian inference, including posterior inference and design, and applications in biostatistics and bioinformatics.
- Integral diffusion (Levy) processes; free boundary problem of fractional diffusion nature, fully nonlinear fractional diffusion models.
- Study of regularity, stability, and instability in fluid mechanics at different scales. It includes: Regularity and partial regularity for Navier-Stokes and kinetic equations;
- Stability for conservation laws and compressible models; Instability and regularity for incompressible and turbulence flows.
The research has direct applications to the formulation, interpretation, and assessment of model non-linear phenomena on multiple dimensional spatial and temporal scales in very diverse geometrical configurations, and to their accurate and efficient approximation using high-performance computing.